Estimating the range of a polynomial on an interval with relative accuracy ε is NP-hard for ε ≤ 1 and feasible for ε > 1
V. Kreinovich1, S.P. Shary2
1University of Texas at El Paso, El Paso, USA
2Federal Research Center for Information and Computing Technologies, Novosibirsk, Russia
Keywords: interval, polynomial, range, NP-hard problem, feasible problem, Gaganov theorem
Abstract
In many practical situations, we need to compute an enclosure for the range of a polynomial in several variables f(x1,…,xn) on given intervals [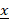 1, 1, 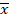 1],...,[ 1],...,[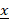 n, n, 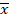 n] with a certain relative accuracy ε > 0. It was known that this problem is NP-hard for all ε < 1/8, but it was not known whether the problem is NP-hard for the other values of ε. Our article provides an almost complete answer to this question, namely, we prove that the problem under study is NP-hard for all ε ≤ 1 and feasible (polynomially complex) for all ε > 1. n] with a certain relative accuracy ε > 0. It was known that this problem is NP-hard for all ε < 1/8, but it was not known whether the problem is NP-hard for the other values of ε. Our article provides an almost complete answer to this question, namely, we prove that the problem under study is NP-hard for all ε ≤ 1 and feasible (polynomially complex) for all ε > 1.
|



