|
|
2025 year, number 3
|
A.L. Ageev, T.V. Antonova
N.N. Krasovsky Institute of Mathematics and Mechanics, Ural Branch of the Russian Academy of Sciences, Yekaterinburg, Russia
Keywords: ill-posed problems, regularization method, discontinuity lines, global localization, discretization, separability threshold, image separation
Abstract >>
We consider the ill-posed problem of localizing (finding the position of) the discontinuity lines of a function of two variables, provided that outside the discontinuity lines the function satisfies a Lipschitz condition, and at each point on the lines there is a discontinuity of the first kind. For a uniform grid with step τ, it is assumed that at each node the mean values of the perturbed function on a square with side τ are known, and the perturbed function approximates the exact function in L2(ℝ2). The level of perturbation δ is assumed to be known. We propose a new approach to construct regularizing algorithms for localizing the discontinuity lines based on a separation of the original noisy data. New algorithms are constructed for a class of functions with piecewise linear discontinuity lines and a convergence theorem with estimates of approximation accuracy is proved.
|
|
N.A. Artyomova1, O.V. Ushakova1,2
1N.N. Krasovsky Institute of Mathematics and Mechanics, Ural Branch of the Russian Academy of Sciences, Yekaterinburg, Russia
2Ural Federal University named after the First President of Russia B.N. Yeltsin, Yekaterinburg, Russia
Keywords: structured grids, deformed volumes, optimal grids, moving grids
Abstract >>
A morphing algorithm included in a three-dimensional structured grid generation technology designed for the numerical solution of differential equations modeling vortex processes in multi-component hydrodynamics is described. The algorithm is intended for the generation of structured grids of a special topology in volumes obtained by deformation of volumes of revolution by the bodies formed by surfaces of revolution with parallel axes. The algorithm is developed by using a variational approach for constructing optimal grids and is a non-stationary one: at each iteration the form of a domain and the grid for it are deformed. Then the grid is optimized in accordance with the following optimality criterion: the closeness of the grid to a uniform and orthogonal one. The iterations are continued up to a given degree of deformation. The algorithm allows one to construct grids in domains of very complex geometry, and it is not necessary to describe the boundary of a complex domain, it is sufficient to describe the volume of revolution, the deforming volume, and the parameters of deformation. Examples of grid calculations are given.
|
|
E.K. Guseva1,2, V.I. Golubev3, V.P. Epifanov2, I.B. Petrov3
1Moscow Institute of Physics and Technology (State University, Dolgoprudny, Russia
2Ishlinsky Institute for Problems in Mechanics of the Russian Academy of Sciences, Moscow, Russia
3Moscow Institute of Physics and Technology (State University), Dolgoprudny, Russia
Keywords: ice rheology, elastoplasticity, fracturing, hydrostatic core, nonlinear waves
Abstract >>
During dynamic loading, ice demonstrates complex nonlinear behavior, which depends on many factors, including strain rate. In practical applications, low-speed collision processes occur, in which ice exhibits both viscous and brittle properties. To consider the specifics of local ice failure, a compound model is proposed in this paper, which distinguishes a hydrostatic core and an elastoplastic zone in ice, with the material far from the impact area in the elastic state. Additionally, volumetric cracking is considered. The model is verified by comparing the results of numerical computations and a laboratory experiment with a spherical indenter. The numerical results demonstrate various phenomena observed in the experiments. The simulations reconstruct nonlinear waves, different destruction patterns, and show the wave nature of fracturing. The deformation curves calculated confirm the possibility of a qualitative description of ice behavior during the main stage of the collision.
|
|
Kh.D. Ikramov
Lomonosov Moscow State University, Moscow, Russia
Keywords: unitoid, cosquare, canonical form with respect to congruences, canonical angles, congruence orbit
Abstract >>
It is well known that if diagonalizable matrices A and B commute, then they can be brought to diagonal form via one and the same similarity transformation. We prove an analog of this statement related to nonsingular unitoid matrices and Hermitian congruence transformations. A matrix is said to be unitoid if it can be brought to diagonal form via a congruence transformation.
|
|
V. Kreinovich1, S.P. Shary2
1University of Texas at El Paso, El Paso, USA
2Federal Research Center for Information and Computing Technologies, Novosibirsk, Russia
Keywords: interval, polynomial, range, NP-hard problem, feasible problem, Gaganov theorem
Abstract >>
In many practical situations, we need to compute an enclosure for the range of a polynomial in several variables f(x1,…,xn) on given intervals [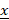 1, 1, 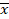 1],...,[ 1],...,[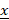 n, n, 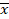 n] with a certain relative accuracy ε > 0. It was known that this problem is NP-hard for all ε < 1/8, but it was not known whether the problem is NP-hard for the other values of ε. Our article provides an almost complete answer to this question, namely, we prove that the problem under study is NP-hard for all ε ≤ 1 and feasible (polynomially complex) for all ε > 1. n] with a certain relative accuracy ε > 0. It was known that this problem is NP-hard for all ε < 1/8, but it was not known whether the problem is NP-hard for the other values of ε. Our article provides an almost complete answer to this question, namely, we prove that the problem under study is NP-hard for all ε ≤ 1 and feasible (polynomially complex) for all ε > 1.
|
|
N. Saha1, J. Shahni1, R. Singh1, V. Guleria2, N. Sriwastav3
1Department of Mathematics, Birla Institute of Technology Mesra, Ranchi, India
2Department of Applied Science and Humanities, National Institute of Advanced Manufacturing Technology Hatia, Ranchi, India
3Department of Mathematics, Chandigarh University, Mohali, India
Keywords: Emden-Fowler equation, Legendre wavelet, Haar wavelet, uniqueness of solution, integral equation, collocation method
Abstract >>
Emden-Fowler-type equations are widely used in mathematical and physical modeling. They describe phenomena in various fields, including astrophysics, quantum mechanics, and nonlinear dynamics. Applications range from modeling stars' thermal behavior to species' distribution in a chemical reaction. Researchers continuously seek new methods to solve Emden-Fowler (EF)-type equations more efficiently and accurately due to their versatility and richness. This article presents a novel approach for solving the generalized EF equations subject to boundary conditions using the Legendre wavelet. First, we convert the problem into equivalent Fredholm integral equations. Next, we use a Legendre wavelet collocation approach and a Newton-Raphson iterative technique to solve the resulting integral equations. The formulation of the proposed algorithm is further supported by its convergence and error analysis. We examine the accuracy of the method by computing the numerical solution and errors for various examples. We compare our numerical outcomes to exact solutions and those achieved by techniques in the literature, such as the Haar wavelet and an optimal homotopy analysis method. The Legendre wavelet collocation method offers superior accuracy with fewer collocation points, making it advantageous.
|
|
M.Y. Sakhno
Omsk Branch of Sobolev Institute of Mathematics, Siberian Branch of the Russian Academy of Sciences, Omsk, Russia
Keywords: genetic algorithm, optimized crossover, adaptive scheme, parallelizable job, energy, schedule
Abstract >>
Some scheduling problems taking into account energy consumption are considered. Such problems arise in multiprocessor computer systems and take into account resource constraints and parallelization capabilities. For these problems, some algorithms of greedy and list types with guaranteed accuracy estimates in the worst case are known. In this paper, we propose an adaptive genetic algorithm with decoding solutions based on the specifics of the problem statements. A peculiarity is that the crossover operator solves a problem of optimal recombination in full and truncated versions. The call of the crossover operators is implemented adaptively. The categorical and numerical parameters are adjusted adaptively by using modern packages. The results of an experimental study show a statistically significant advantage over the known algorithms on a series of problems of different structure.
|
|



