Оценивание на интервале области значений полинома с относительной погрешностью ε является NP-трудным при ε ≤ 1 и полиномиально сложным при ε > 1
В. Крейнович1, С.П. Шарый2
1University of Texas at El Paso, El Paso, USA
vladik@utep.edu
2Федеральный исследовательский центр информационных и вычислительных технологий, Новосибирск, Россия
shary@ict.nsc.ru
Ключевые слова: интервал, полином, область значений, NP-трудная задача, полиномиально сложная задача, теорема Гаганова
Страницы: 293-303
Аннотация
Во многих практических ситуациях необходимо вычислять внешнюю оценку для области значений полинома от нескольких переменных f(x1,…,xn) на заданных интервалах [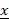 1, 1, 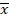 1],...,[ 1],...,[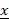 n, n, 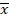 n] с определённой относительной погрешностью ε > 0. Известно, что эта задача является NP-трудной для всех ε < 1/8, но не было известно, является ли задача NP-трудной для других значений ε. В нашей статье даётся полный ответ на этот вопрос, а именно, мы доказываем, что рассматриваемая задача является NP-трудной для всех ε ≤ 1 и полиномиально разрешима для всех ε > 1. n] с определённой относительной погрешностью ε > 0. Известно, что эта задача является NP-трудной для всех ε < 1/8, но не было известно, является ли задача NP-трудной для других значений ε. В нашей статье даётся полный ответ на этот вопрос, а именно, мы доказываем, что рассматриваемая задача является NP-трудной для всех ε ≤ 1 и полиномиально разрешима для всех ε > 1.
DOI: 10.15372/SJNM20250305
EDN: OLQSLH
|



